Domains

The domain of an expression is the set of the possible values of that expression.

A domain is represented by a domain expression. For example:

  • "Integers"
  • "Booleans"
  • ["FunctionOf", "Integers", "Integers"]

A domain expression is either a domain literal represented by an identifier such as "Integers" and "Booleans" or a constructed domain represented by a function expression.

Of course, it wouldn’t make sense for it to be any function, so the name of that function must be among a limited set of domain constructors.

This effectively defines a specialized language to represent domains. In some cases the same function name can be used in a domain expression and a value expression, but they will be interpreted differently.

Domains are similar to types in programming languages. Amongst other things, they are used to select the correct function definition.

For example a function Add could have several implementation to operate on numbers or on matrixes. The domain of the arguments would be used to select the appropriate function definition.

Symbolic manipulation algorithms also use domains to decide when certain transformations are applicable.

For example, \( \sqrt{x^2} = x\) only if \(x \geq 0\)

Read more about the Domain Literals included in the standard library of the Compute Engine

Obtaining the Domain of an Expression

To query the domain of an expression read the domain property of the expression.

ce.box("Pi").domain;
// ➔ "TranscendentalNumbers"

ce.box("Divide").domain;
// ➔ '["FunctionOf",  "Numbers", "Numbers", "Numbers]':
//   domain of the function "Divide"

ce.box(["Add", 5, 2]).domain;
// ➔ "Numbers": the result of the "Add" function
//   (its codomain) belongs to the domain "Numbers"

ce.box(["Add", 5, 2]).evaluate().domain;
// ➔ "Integers": once evaluated, the domain of
//   the result may be more specific

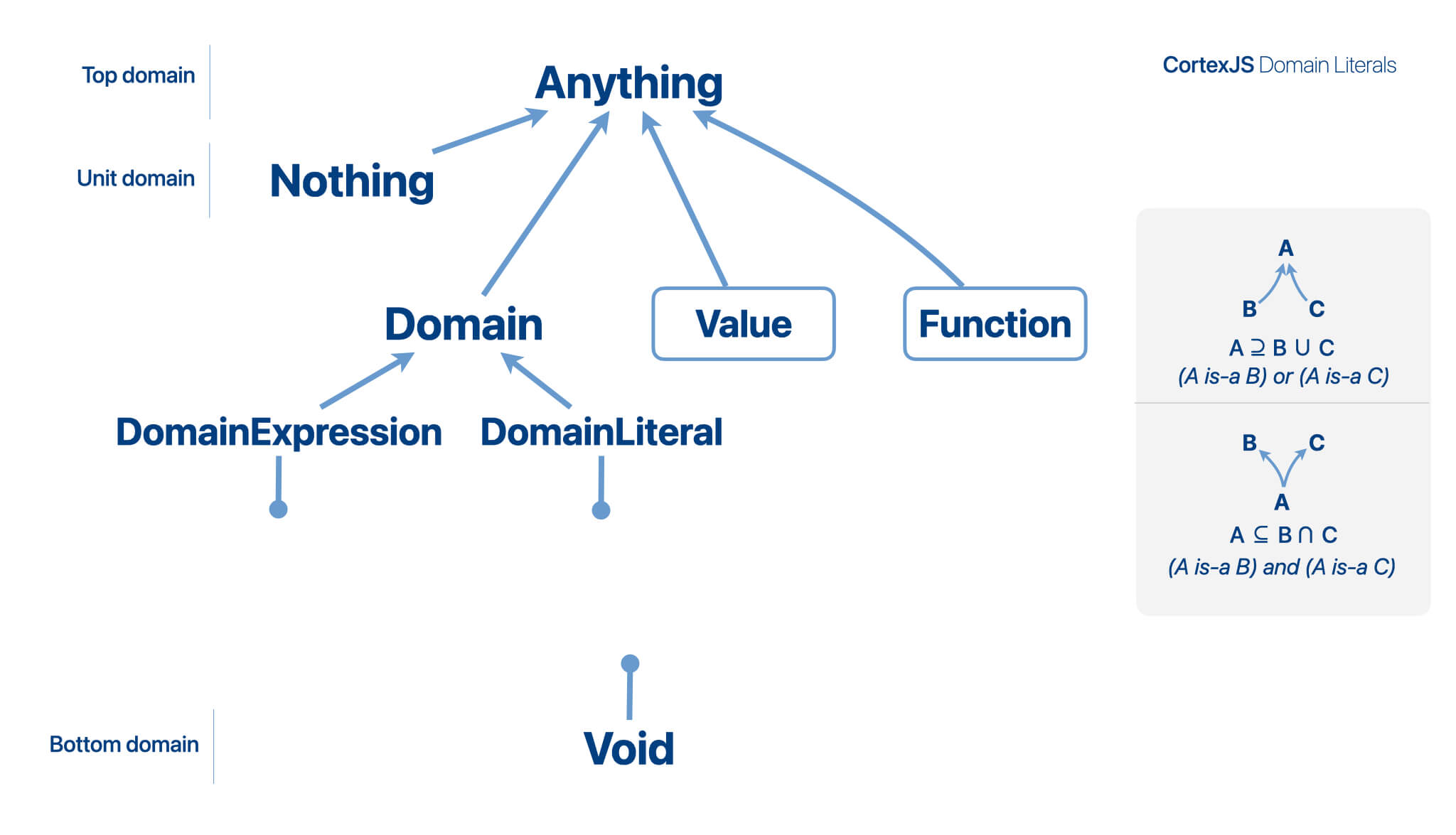
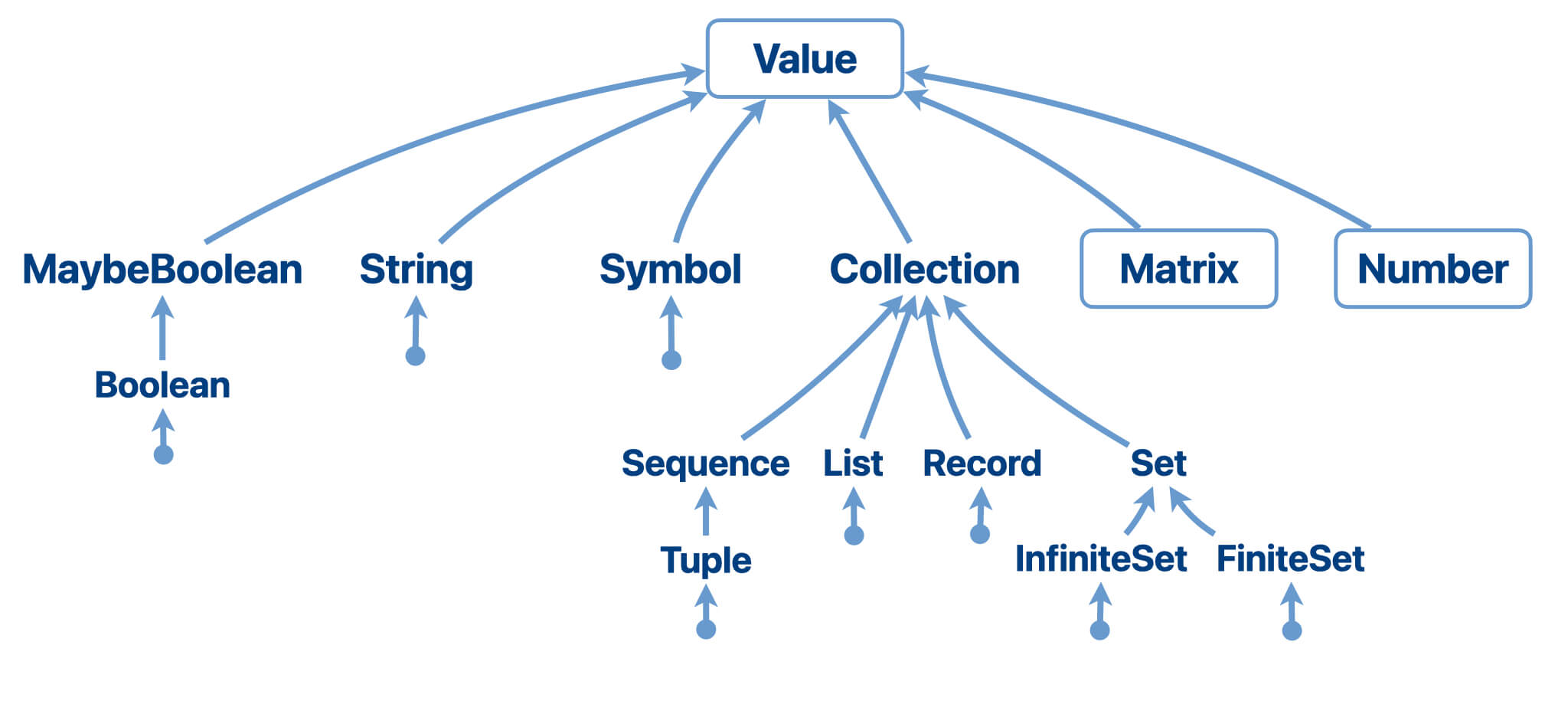
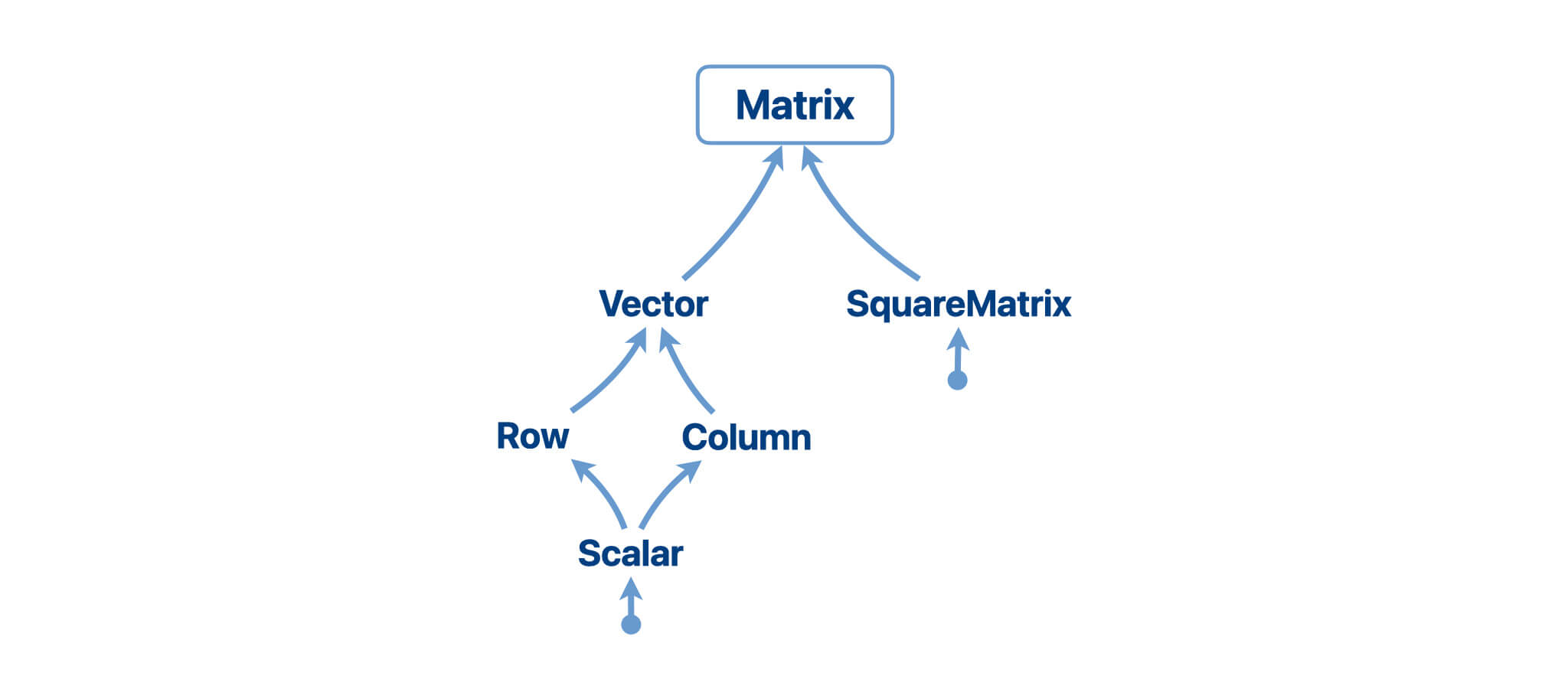
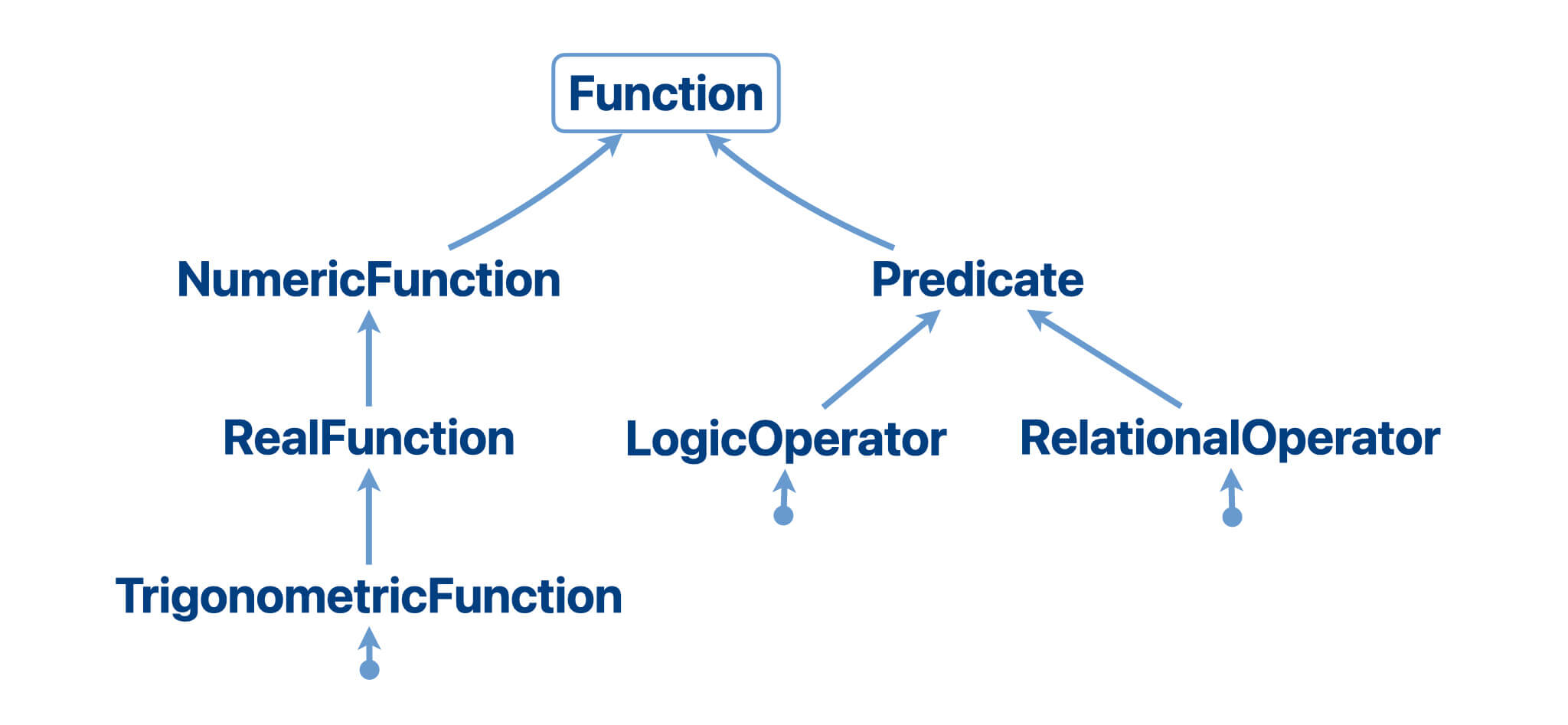
Domain Lattice

Domains are defined in a hierarchy (a lattice). The upper bound of the domain lattice is the Anything domain (the top domain) and its lower bound is the Void domain (the bottom domain).

  • The Anything domain contains all possible values and all possible domains. It is used when not much is known about the possible value of an expression. In some languages, this is called the universal type.
  • The Void domain contains no value. It is the subdomain of all domains. Also called the zero or empty domain. It is rarely used, but it could indicate the return domain of a function that never returns. Not to be confused with Nothing, which is used when a function returns nothing.

There are a few other important domains:

  • The Domains domain contains all the domain expressions.
  • The Values domain contains all the expressions which are not domains,
    for example the number 42, the symbol alpha, the expression ["Add", "x", 1].
  • The Nothing domain has exactly one value, the symbol Nothing. It is used when an expression has no other meaningful value. In some languages, this is called the unit type and the unit value. For example a function that returns nothing would have a return domain of Nothing and would return the Nothing symbol.

The parent of a domain represents a is-a/subset-of relationship, for example, a List is-a Collections.

Anything domains

Values domains

Tensor domains

Function domains

Numbers domains

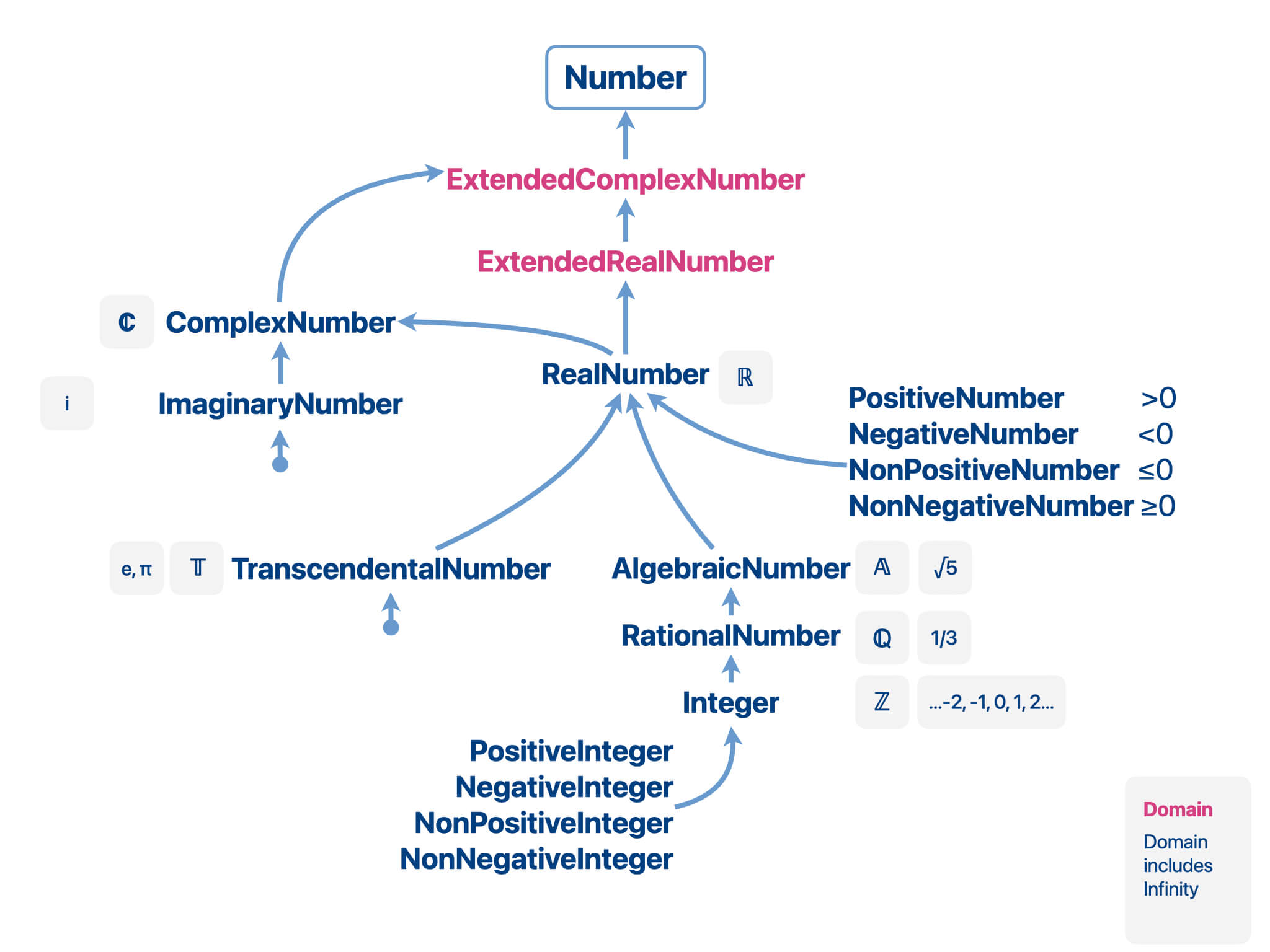
The implementation of the CortexJS domains is based on Weibel, Trudy & Gonnet, Gaston. (1991). An Algebra of Properties… 352-359. 10.1145/120694.120749. .

Domain Compatibility

Two domains can be evaluated for their compatibility.

There are three kinds of compatibility that can be determined:

  • Invariance: two domains are invariant if they represent exactly the same set of values
  • Covariance: domain A is covariant with domain B if all the values in A are also in B. For example Integers is covariant with Numbers
  • Contravariant: domain A is contravariant with domain B if all the values in B are in A. For example Anything is contravariant with every domain.

To evaluate the compatibility of two domains use domain.isCompatible()

By default, domain.isCompatible() will check for covariant compatibility.

ce.domain("PositiveNumbers").isCompatible("Integers");
// ➔ true

ce.domain("Numbers").isCompatible("RealNumbers", "contravariant");
// ➔ true

Constructing New Domains

A domain constructor is a function expression with one of the identifiers below.

To define a new domain use a domain constructor.

// Functions with a single real number argument and that return an integer
["FunctionOf", "RealNumbers", "Integers"]

When a domain expression is boxed, it is automatically put in canonical form.

Domain Constructor Description
FunctionOf ["FunctionOf", ...<arg-domain>, <co-domain>]
For example, ["FunctionOf", "Numbers", "Booleans"] is the domain of the functions that have a single argument, a number, and return a boolean (has a boolean codomain).
By default, compatibility is determined by using covariance for the arguments and contravariance for the co-domain.
ListOf ["ListOf", <element-domain>]
TupleOf ["TupleOf", <element-1-domain>], ["TupleOf", <element-1-domain>] ... <element-n-domain>]
Intersection ["Intersection", <domain-1>, <domain-2>]
All the values that are a member of <domain-1> and <domain-2>
Union ["Union", <domain-1>, <domain-2>]
All the values that are a member of <domain-1> or <domain-2>
OptArg ["OptArg", <domain>]
A value of <domain> or Nothing
VarArg ["VarArg", <domain>]
As a function argument zero or more values of <domain>.
Head
Symbol
Literal This constructor defines a domain with a single value, the value of its argument. ` |
Covariant
Contravariant
Invariant ["Invariant", <domain>]
This constructor indicate that a domain is compatible with this domain only if they are invariants with regard to each other.
Multiple ["Multiple", <factor>, <domain>, <offset>]
The set of numbers that satisfy <factor> * x + <offset> with x in domain. For example, the set of odd numbers is ["Multiple", 2, "Integers", 1]